Brojni sustavi i pojmovi

Tri glavna područja razlike od naših brojeva

Zamislite koliko bi bilo lakše naučiti aritmetiku u ranim godinama kada bi sve što ste trebali naučiti pisati liniju kao što sam ja i trokut. To su u osnovi morali učiniti svi drevni ljudi Mezopotamije, iako su ih tu i tamo varirali, izduživali, okretali se itd.

Nisu imali naše olovke i olovke ili papir za tu stvar. Ono s čim su pisali bilo je sredstvo koje će se koristiti u skulpturi, jer je medij glina. Je li ovo teže ili lakše naučiti rukovati nego olovku, to je izbacivanje, no zasad su naprijed u odjelu za lakoću, sa samo dva osnovna simbola koja se mogu naučiti.

Sljedeći korak baca ključ u odjel za jednostavnost. Koristimo a

U "Počast Babiloniji" [Matematički glasnik, Vol. 76, br. 475, "Upotreba povijesti matematike u nastavi matematike" (ožujak, 1992.), str. 158-178], učitelj pisac Nick Mackinnon kaže da koristi babilonsku matematiku kako bi podučavao 13-godišnjake o bazama koje nisu 10. Babilonski sustav koristi bazu-60, što znači da je umjesto decimalnog značaja seksualan.

I babilonski brojni sustav i naš oslanjaju se na položaj kako bi dali vrijednost. Dva sustava to rade različito, dijelom i zato što njihovom sustavu nedostaje nula. Učenje babilonskog sustava s lijeva na desno (visoko na nisko) za prvi ukus osnovne aritmetike vjerojatno više nije teško nego naučiti naš dvosmjerni, pri čemu moramo zapamtiti redoslijed decimalnih brojeva - povećavajući se iz decimalnog, one, desetine, stotine, a zatim navijaju u drugom smjeru s druge strane, ni jedan stupac, samo desetine, stotinke, tisućama itd.

Precizat ću na stavove babilonskog sustava na daljnjim stranicama, ali prvo treba naučiti nekoliko važnih brojevnih riječi.

Govorimo o razdobljima godina koristeći decimalne veličine. Imamo desetljeće za 10 godina, stoljeće za 100 godina (10 desetljeća) ili 10X10 = 10 godina u kvadratu, a tisućljeće za 1000 godina (10 stoljeća) ili 10X100 = 10 godina u kubama. Ne znam neki viši pojam od toga, ali to nisu jedinice koje su Babilonci koristili. Nick Mackinnon odnosi se na tablet iz Senkareha (Larsa) od sir Henryja Rawlinsona (1810-1895) * za jedinice koje su Babilonci koristili, a ne samo za uključene godine, već i za podrazumijevane količine:

1. soss
2. NER
3. sar.

sossnersosssarsoss

Još uvijek nema prekidača za kravate: Nije nužno lakše naučiti izvedene izraze u obliku kvadrata i kockica s latinskog nego što je to jednosložni babilonski jezik koji ne uključuje kockanje, nego množenje s 10.

Što misliš? Da li bi bilo teže naučiti osnove broja kao babilonsko školsko dijete ili kao moderni učenik u školi koja govori engleski jezik?

* George Rawlinson (1812.-1902.), Henryjev brat, pokazuje pojednostavljenu prepisanu tablicu kvadrata u Sedam velikih monarhija drevnog istočnog svijeta. Čini se da je tablica astronomska, temelji se na kategorijama babilonskih godina.

Sve fotografije potječu iz ove skenirane verzije izdanja Georgea Rowlinsona iz 19. stoljeća Sedam velikih monarhija drevnog istočnog svijeta.

Budući da smo odrasli s drugačijim sustavom, babilonski brojevi zbunjuju.

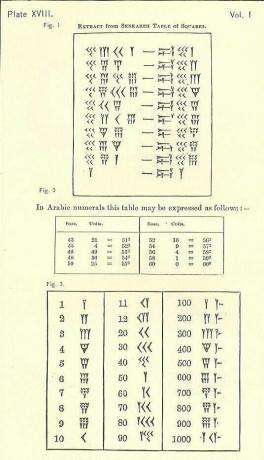
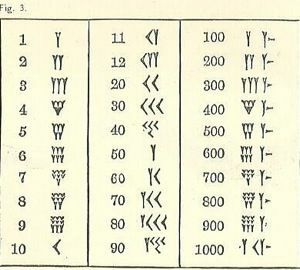
Barem se brojevi kreću od visokog s lijeva do niskog s desne strane, poput našeg arapskog sustava, ali ostatak će se vjerojatno činiti nepoznatim. Simbol za jedan je klinast ili Y-oblik. Nažalost, Y također predstavlja 50. Postoji nekoliko zasebnih simbola (svi na temelju klina i crte), ali svi ostali brojevi formirani su od njih.

Sjetite se oblika pisanja klinasto pismo ili u obliku klina. Zbog alata koji se koristi za crtanje linija postoji ograničena raznolikost. Klin može ili ne mora imati rep, izvučen povlačenjem kvačice za pisanje duž gline nakon utiskivanja dijela trokuta na dio.

10, opisano kao strelica, izgleda pomalo kao

Tri retka do 3 mala 1 (napisana kao Ys sa skraćenim repovima) ili 10s (10 je napisano kao

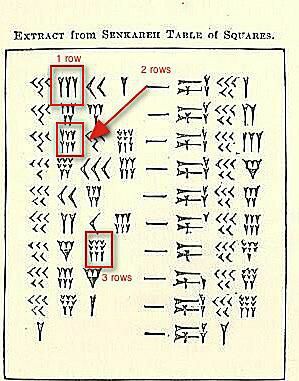
Postoje tri skupa klinastog broja klasteri istaknuto na gornjoj slici.

Trenutno se ne bavimo njihovom vrijednošću, već demonstriranjem kako biste vidjeli (ili napisali) bilo gdje od 4 do 9 istog broja grupiranog zajedno. Tri idu redom. Ako postoji četvrti, peti ili šesti, to ide ispod. Ako postoji sedmi, osmi ili deveti, trebat će vam treći red.

Sljedeće stranice nastavljaju se s uputama za provođenje proračuna babilonskim kinoformom.

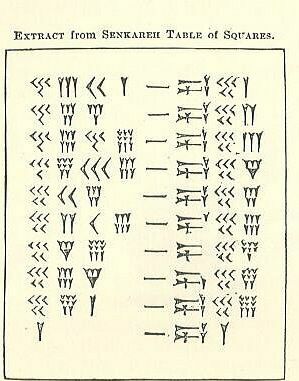
Iz onoga što ste pročitali gore o časopisu soss - kojega ćete pamtiti je babilonski 60 godina, klin i strijela - koji su opisni nazivi za klijentske tragove, pogledajte možete li shvatiti kako funkcioniraju ti proračuni. Na jednoj je strani crtica slična broju, a na drugoj je kvadrat. Probajte to kao grupa. Ako ne možete shvatiti, pogledajte sljedeći korak.

Možete li to sad shvatiti? Dajte priliku.

...

Na lijevoj strani su 4 jasna stupca, a iza njih je znak crtice i s desne strane 3 stupca. Gledajući s lijeve strane, ekvivalent stupcu 1s su zapravo 2 stupca najbliža "crtici" (unutarnjim stupcima). Ostala 2, vanjska stupca broje se zajedno kao stupac 60-ih.

• Četverac
• 3-Ys = 3.
• 40+3=43.
• Jedini problem ovdje je što je iza njih još jedan broj. To znači da nisu jedinice (mjesto onih). 43 nisu 43-oni, već 43-60-ti, jer je spolni (osnovni-60) sustav i nalazi se u soss stupac kao što pokazuje donja tablica.
• Pomnožite 43 sa 60 da biste dobili 2580.
• Dodajte sljedeći broj (2-
• Sada imate 2601.
• To je kvadrat od 51.

Sljedeći red sadrži 45 u soss pa pomnožite 45 sa 60 (ili 2700), a zatim dodate 4 iz stupca jedinica, pa imate 2704. Kvadratni korijen iz 2704. iznosi 52.

Možete li shvatiti zašto je posljednji broj = 3600 (60 u kvadratu)? Savjet: Zašto to nije 3000?